7장 - 관계 데이터 연산

출처 : http://www.kocw.net/home/cview.do?lid=d24b99ec023b8c09

데이터베이스의 원리와 응용

 

 

이번 시간에는 관계 데이터 연산에 대해 학습한다.

1. 관계 데이터 연산의 개념
2. 관계 대수

 

 

학습목표

• 관계 데이터 연산의 개념과 종류를 알아본다.
• 일반 집합 연산자와 순수 관계 연산자의 차이를 이해한다.
• 일반 집합 연산자와 순수 관계 연산자를 이용해 질의를 표현하는 방법을 익힌다.

 

 

관계 데이터 연산의 개념

• 데이터 모델은 데이터 구조와 연산, 제약조건으로 구성된다.
• 이전에 우리가 데이터 구조와 제약조건은 살펴보았다. 이번 시간에는 연산에 초점을 맞춰서 진행한다.

 

 

관계 데이터 연산(Relational Data Operation)

• 원하는 데이터를 얻기 위해 릴레이션에 필요한 처리 요구를 수행하는 것
• 관계 대수와 관계 해석이 있다.
  • 기능과 표현력 측면에서 능력이 동등함
  • 처리절차를 얼마나 자세히 기술하느냐에 따라 차이를 보인다.
• 관계 데이터 연산은 관계 대수와 관계 해석으로 나눌 수 있다.
  • 관계 대수 : 원하는 결과를 얻기 위해 데이터 처리 과정을 순서대로 기술하는 절차적 언어
    • 대표적인 연산 : 선택(Selection), 투영(Projection), 조인(Join), 합집합, 교집합, 차집합 등
  • 관계 해석 : 원하는 결과를 얻기 위해 처리를 원하는 데이터가 무엇인지만 기술하는 비절차적 언어
    • 대표적인 연산 : 튜플 변수, 원자 공식, 양화기 등
• 관계 데이터 연산이 필요한 이유
  • 데이터 조회 : 특정 조건에 맞는 데이터만 추출하거나, 여러 테이블의 데이터를 결합하여 새로운 정보를 생성할 수 있다.
  • 데이터 수정 : 데이터를 추가, 삭제, 수정하는 작업을 수행할 수 있다.
  • 데이터 분석 : 데이터를 분석하여 통계 정보를 얻거나, 특정 패턴을 찾아낼 수 있다.

 

 

관계 대수

관계 대수(Relational Algebra)의 개념

• 원하는 결과를 얻기 위해 릴레이션의 처리 과정을 순서대로 기술하는 절차적 언어
• 릴레이션을 처리하는 연산자들의 모임
  • 일반 집합 연산자와 순수 관계 연산자로 분류된다.
• 폐쇄 특성(closure property)이 존재한다.
  • 피연산자도 릴레이션이고 연산의 결과도 릴레이션이다. 즉, 관계 대수에서 어떤 연산을 수행하든지 간에 그 결과는 항상 테이블 형태로 나타낼 수 있는 관계(릴레이션)이라는 뜻이다.

 

관계 대수의 장점

• 명확하고 간결한 표현 : 수학적인 기호를 사용하여 복잡한 질의를 간결하게 표현할 수 있다.
• 다양한 데이터베이스 시스템에 적용 가능 : 관계형 데이터베이스 모델을 따르는 모든 시스템에서 사용할 수 있다.

관계 대수의 단점

• 효율성 문제 : 복잡한 질의의 경우, 관계 대수 표현식을 최적화하는 것이 어려울 수 있다.

 

 

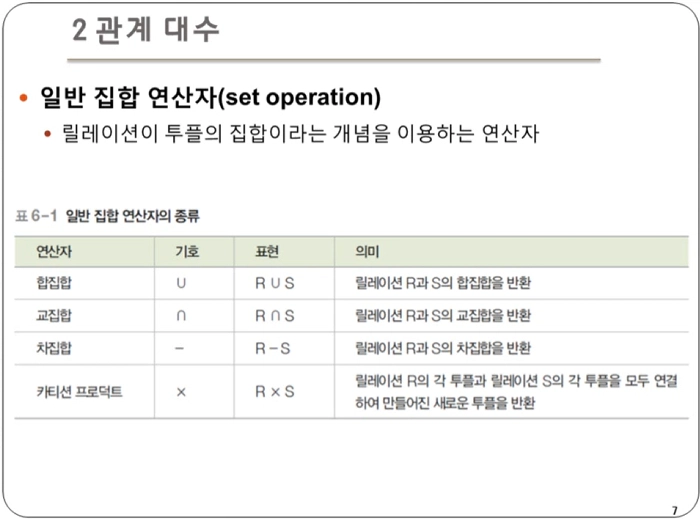
일반 집합 연산자(Set Operation)

• 릴레이션이 튜플의 집합이라는 개념을 이용하는 연산자

 

 

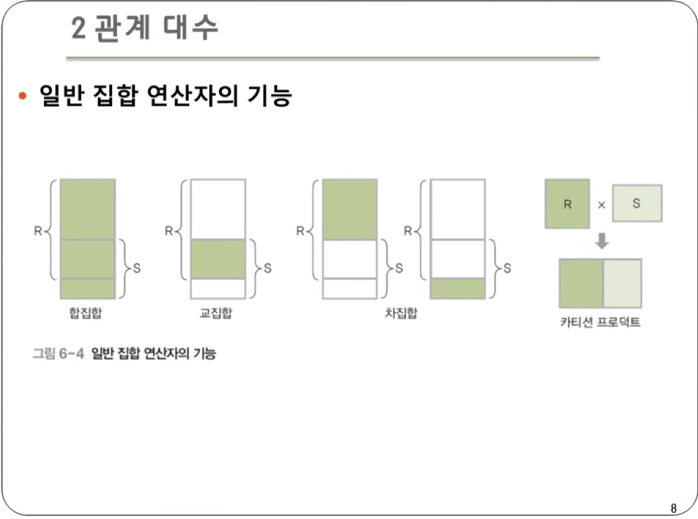
• 크게 4 종류의 연산자가 존재한다.
  • 합집합 : 릴레이션 R과 S의 합집합을 리턴
    • 데이터 통합 : 여러 테이블의 데이터를 하나로 합쳐 분석하기 위한 기반을 제공한다.
    • 조건 : 두 릴레이션의 속성 개수와 도메인이 같아야 한다.
  • 교집합 : 릴레이션 R과 S의 교집합을 리턴
    • 중복 데이터 제거 : 교집합을 이용하여 중복된 데이터를 찾아 제거할 수 있다.
    • 조건 : 합집합과 동일하게 속성 개수와 도메인이 같아야 한다.
  • 차집합 : 릴레이션 R과 S의 차집합을 리턴
    • 데이터 비교 : 차집합을 이용하여 두 테이블의 차이점을 파악할 수 있다.
    • 조건 : 합집합과 동일하게 속성 개수와 도메인이 같아야 한다. 

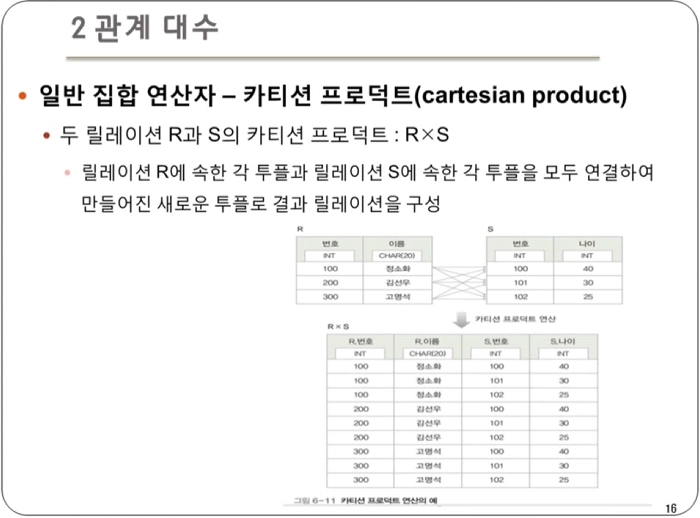
• 카티션 프로덕트 : 두 릴레이션에 있는 모든 튜플을 가능한 모든 조합으로 연결하여 새로운 튜플을 리턴
  • 데이터 조작 : 카티션 프로덕트를 이용하여 새로운 관계를 만들고, 다른 연산자와 조합하여 복잡한 질의를 수행할 수 있다.
  • 결과 릴레이션 특성
    • 차수(열 degree)는 릴레이션 R과 S의 차수를 더한 것과 같다.
    • 카디널리티(행 cardinality)는 릴레이션 R과 S의 카디널리티를 곱한 것과 같다.
  • 교환적 특징이 있다.
    • R x S = S x R
  • 결합적 특징이 있다.
    • (R x S) x T = R x (S x T)

 

일반 집합 연산자의 특성

• 피연산자가 2개 필요하다.
  • 2개의 릴레이션을 대상으로 연산을 수행
• 합집합, 교집합, 차집합은 피연산자인 두 릴레이션이 합병이 가능해야 한다.
  • 합병 가능(union-compatible) 조건
    • 두 릴레이션의 차수가 같아야 한다.
    • 두 릴레이션에서 서로 대응되는 속성의 도메인이 같아야 한다.

 

 

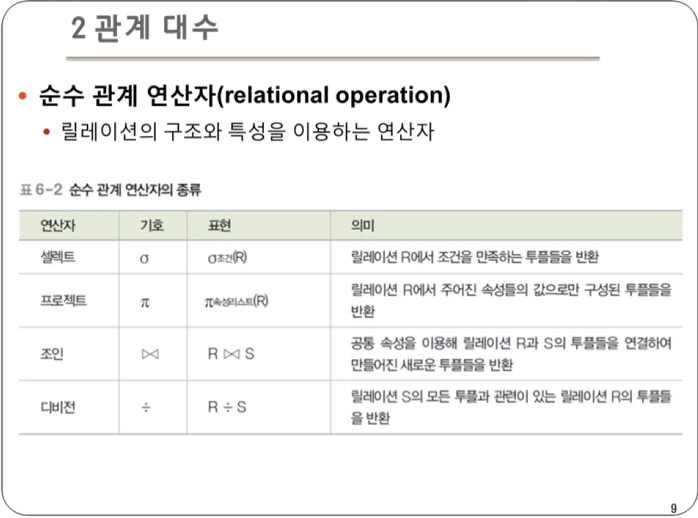
순수 관계 연산자(Relational Operation)

• 릴레이션의 구조와 특성을 이용하는 연산
• 릴레이션의 튜플이나 속성을 기준으로 데이터를 셀렉트, 프로젝트, 조인하는 등 다양한 방식으로 데이터를 조작하는 역할을 한다.

 

 

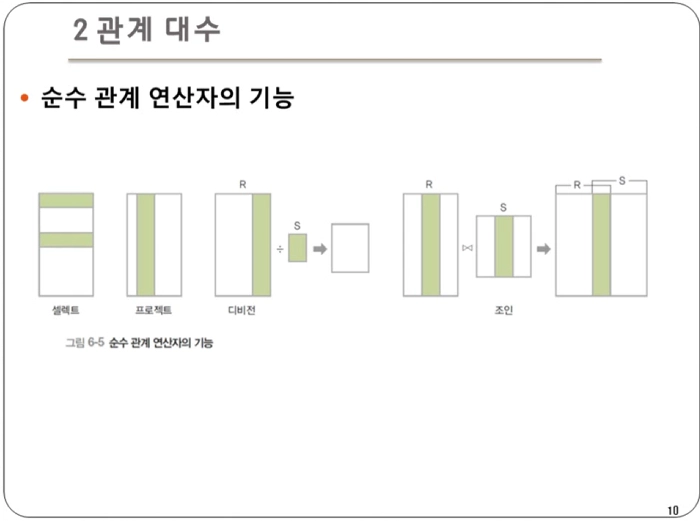
• 크게 4가지의 연산자가 존재한다.

 

 

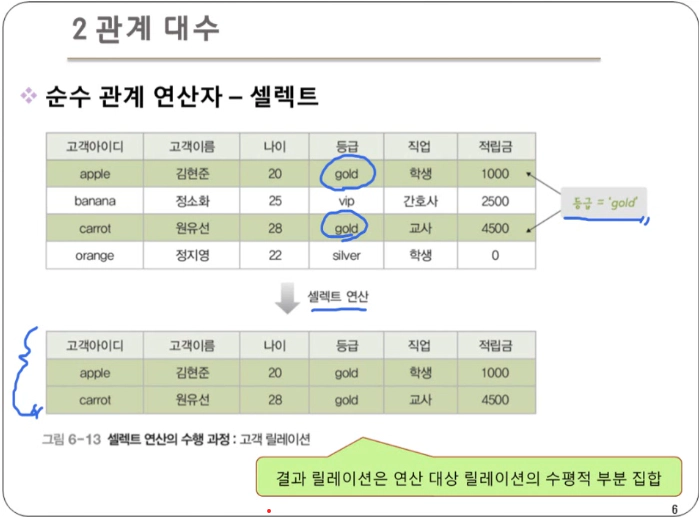
셀렉트 : 릴레이션에서 특정 조건을 만족하는 튜플만 선택하여 결과 릴레이션을 구성

• 하나의 릴레이션을 대상으로 연산을 수행
• 데이터 언어적 표현법 : 릴레이션 where 조건식
• 조건식
  • 비교식, 프레디킷(predicate)이라고도 한다.
  • 속성과 상수의 비교나 속성들 간의 비교로 표현
  • 비교연산자(<, >, =)와 논리연산자를 이용해 작성

 

 

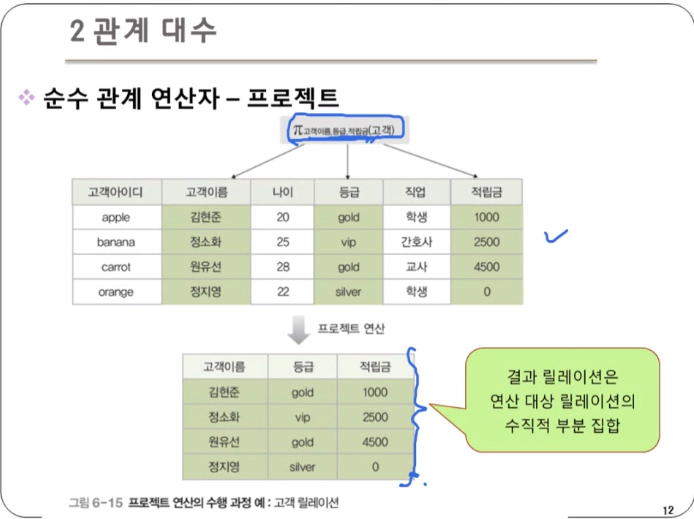
프로젝트 : 릴레이션에서 특정 속성들의 값으로 결과 릴레이션을 구성

• 하나의 릴레이션을 대상으로 연산을 수행
• 데이터 언어적 표현법 : 릴레이션[속성리스트]

 

 

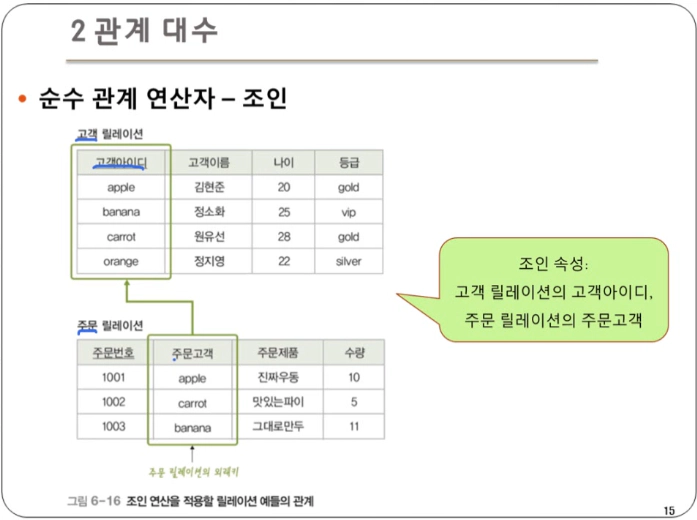
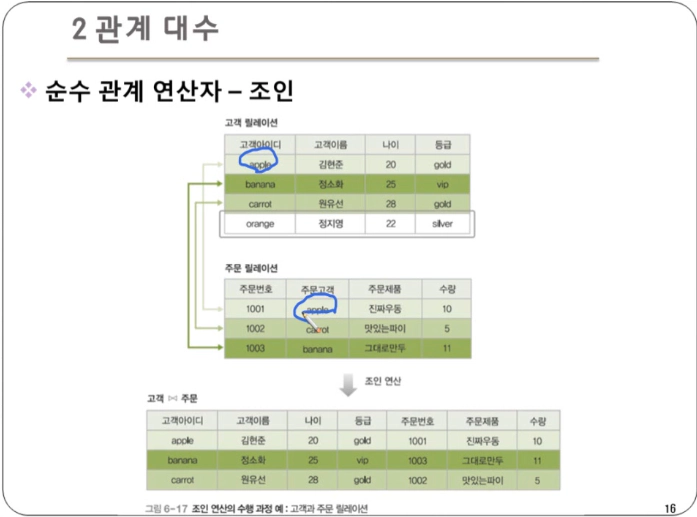
조인 : 두 릴레이션의 공통 속성을 기준으로 튜플들을 연결하여 만들어진 새로운 튜플들을 반환

• 조인 속성의 값이 같은 튜플만 연결하여 생성된 튜플의 결과 릴레이션에 포함
• 조인 속성 : 두 릴레이션이 공통으로 가지고 있는 속성
• 자연 조인(natural join)이라고도 한다.

 

 

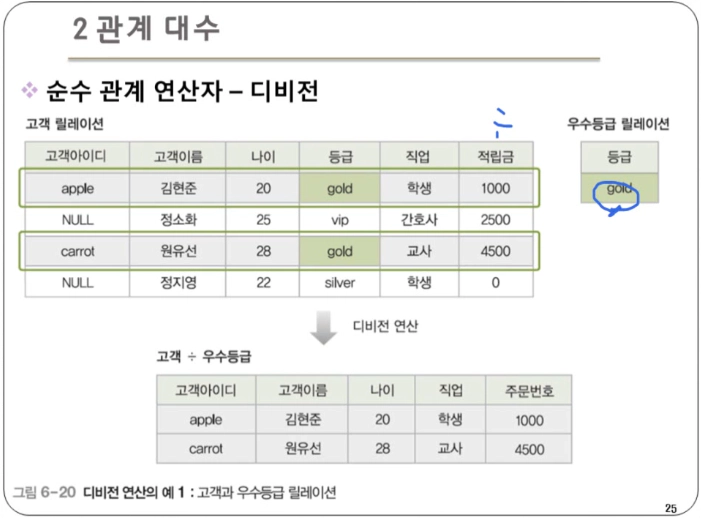
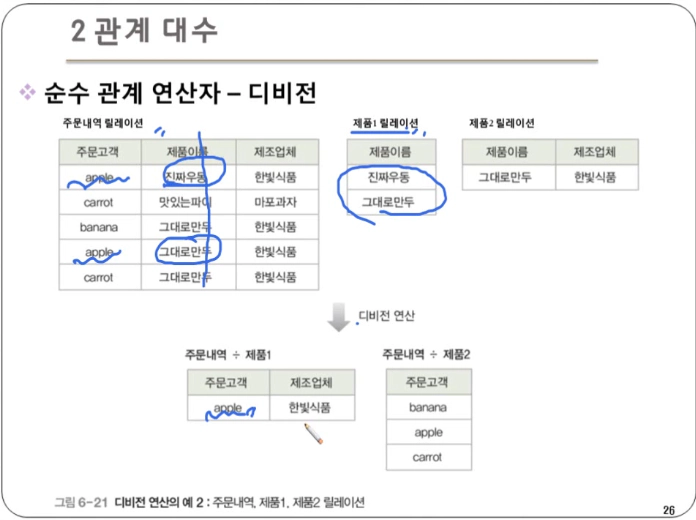
디비전 : 릴레이션2의 모든 튜플과 관련이 있는 릴레이션1의 튜플로 결과 릴레이션을 구성. 즉, 하나의 릴레이션(피제수 R)의 모든 튜플이 다른 릴레이션(제수 S)의 모든 튜플과 연결될 수 있는지 확인하는 연산이다.

• 단, 릴레이션1이 릴레이션2의 모든 속성을 포함하고 있어야 연산이 가능하다.
• 표현법 : 릴레이션1 ÷ 릴레이션2